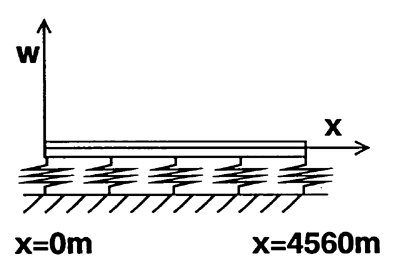
Fig.1 Elastic beam on elastic foundation

ここで、kjは境界条件により決まり、離散的な値をとる。kjl〜jπのオーダーであるので、浮体長lが大きくなるとkjは連続的になる。両端自由の場合は最初の固有値ｋ⁰が0であるために、浮力弾性によるモードがヒーブあるいはピッチの最低次モードとなる6）。ところで、（2）式導出にあたっては、なんら境界条件を用いていないから、零点振動として、

なる振動数があり、いかなる境界条件においても固有振動数はこの値より大きくなる。浮体長ｌが大きくなるとモード固有値が連続的になるので、固有振動数は零点振動から連続的に存在する。さて、式（1）の左辺の内、第3項が落ちた形は真空中での梁の振動方程式である。このとき[慣性項]と［梁剛性の項]の大小関係を表す指標として、

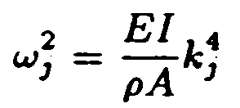
があった。これをバネなし‘固有振動数’と呼んでおく。浮力弾性が存在する場合の‘固有振動数’と厳密に区別する。これは境界条件に依存するため、境界条件に依存しない形、

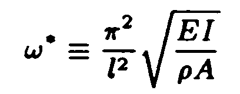
が通常用いられている。同様にω0は［慣性項］と［浮力弾性の項］の大小関係を表す指標である一的の代わりに（1）式の[性項］と［浮力弾性の項＋梁剛性の項]の大小関係すなわち（2）式を用いてもよいが、固有振動数が零点振動から連続的に存在する場合は、零点振動の方が重要である。また零点振動が境界条件によらないのは定義式より明らかである。最後に[浮力弾性の項］と［梁剛性の項]の大小関係を表すパラメータが考えられる。これは先の2つのパラメータと異なり、時間に依存しない。実はこれが鈴木の発見した特性波数、

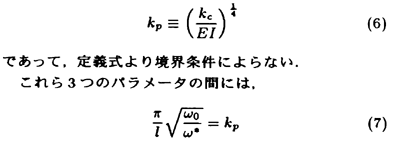
の関係があり、これらの内2つが決まれば残りのパラメータも決まる。特に長大な場合はω.は小さくなり、ωjはω0から連続的に出現する。その結果、周波数特性は、ω0とkpの位置関係とその時の応答を見ればよい。本報告では、特に重要と思われるωp < ω0の場合について議論する。ここでωｐは適当な分散関係を用いてkpを変換したものである。波の周波数ωに対して。ω < ω0なる設計を前提とすると。この領域（波数領域）での応答特性を完全に調べ上げることは重要である。両端自由についての波数領域での解析録6）9）よりkpl > 10では、自由端の変位振幅は、

となる。特にn = 1の時が重要となり、鈴木の特性距離6）の1/4となる。xpeakにおいて曲げ応力に種値を取らせるkpeakを簡単な式で表現するのは、精度との兼ね合い上、難しい。敢えて複雑な式をあげるより。式（13）,（12）を用い、実際にxpeakでの周波数応答の様子を描くことにより、kpeak,Mpeak,σpeakを求める方がよいと思われる。

前ページ　　　目次へ　　　次ページ